Acústica en espacios cerrados – Ondas estacionarias

Por Marcelo Iacovino
Ingeniero de sonido
Titular en INSAM Ingeniería Acústica
Profesor de Acústica en Escuelas Tecson

Antes de comenzar a explicar los pormenores de la acústica dentro de espacios cerrados, me gustaría formular algunas preguntas muy frecuentes:
1. Al momento de grabar una toma de micrófono, ¿notás que el mic captura el instrumento con mucho menos
punch con respecto a cómo se escuchaba con los oídos al natural?
2. El absorbente acústico ¿hizo que la sala se sintiera más muerta y los graves no solo no mejoraron sino que
se volvieron mucho menos definidos?
3. En la sala de mezcla ¿los bajos se escuchan mucho más fuertes en la parte trasera o en las esquinas del
recinto que en el centro? Y como resultado de esto, ¿te das cuenta que nunca estamos seguros sobre cuánto
bajo es suficiente y las consecuencias las notamos a la hora de pasar la mezcla en otro lugar a veces
provocando distorsión y/o volumen general pobre?
4. Al masterizar una canción en el mismo cuarto donde se mezcló, ¿notás que el sonido no parece mejorar
mucho y después de varias pruebas regresamos a la primera curva? ¿O quitamos de plano la ecualización?
5. En salones de baile o en la pista de la discoteca, ¿los bajos son pobres y alrededor o afuera del epicentro
son demasiado fuertes provocando un campo sonoro muy poco uniforme?
Bueno, sí a alguien se les presentó algunos o varios de estos problemas dentro de sus salas, la respuesta es que
estamos ante un problema de ondas estacionarias y para saber cómo solucionarlos, primero hay que
entenderlas.

Entendiendo las ondas estacionarias

Las ondas estacionarias (standing waves) son uno de los enemigos más fuertes y comunes en todo recinto
sonoro.
No importa que tan bueno sea tu equipo, tus monitores, micrófonos e interface, siempre las ondas
estacionarias pueden echar a perder toda la inversión.
A pesar del desconcierto de muchos ingenieros y sonidistas sobre esta problemática, es muy fácil explicar
estos fenómenos. Resulta que las frecuencias graves (notas bajas) reflejan en las paredes y, sin importar los
materiales absorbentes dentro de la sala, al reflejar en las superficies duras “chocan” contra sí mismas
reforzándose en algunos puntos (antinodos), mientras que en otros puntos llamados (nodos) se cancelan. Esto
ocasiona que nuestro cuarto sea como un “queso gruyere”, o sea, lleno de agujeros.

Este fenómeno se debe a que en ciertas partes del cuarto estas ondas reflejadas se suman en “fase” y en otras
“fuera de fase”.

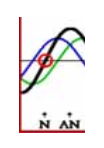
Fig. 1

En esta ilustración apreciamos una onda azul que viaja de izquierda a derecha y otra verde que representa el
“rebote” de la misma en la pared paralela y que se desplaza en sentido contrario. Ambas ondas se suman
creando una onda resultante (en negro). Esta resultante refleja diferentes momentos de la forma en que se
suman la azul y la verde: En fase o máxima presión y fuera de fase (180º) o presión nula.
Cabe notar que los momentos de mayor presión ocurren siempre en los antinodos (AN), mientras que existen
otros puntos, nodos (N), donde la presión es siempre nula.

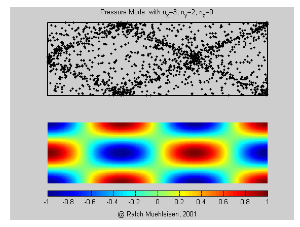
Fig. 2

En esta otra figura más avanzada, podemos apreciar la expansión y compresión de moléculas de aire (puntos negros). En el cuadro inferior las elipses indican los antinodos tornándose de color rojo cuando alcanzan la máxima compresión (positivo) y tornándose azul cuando alcanzan la máxima expansión (negativo). Ambos estados, compresión y expansión, forman los ciclos acústicos de una frecuencia audible y que debido a los rebotes en las paredes son percibidos solamente en estas regiones.
En contraste las zonas verdes o nodos mantienen una presión nula constantemente por lo que el aire no presenta fluctuaciones de presión y como consecuencia el sonido no se produce. Estas zonas también se conocen como puntos muertos, agujeros o dead spots. Cuando encontramos la frecuencia de resonancia exacta de un cuarto, tanto nodos como antinodos permanecen físicamente en el mismo lugar dando origen a las famosas "ondas estacionarias".
En teoría todo es entendible pero, ¿qué efecto tiene esto desde el punto de vista auditivo?

Pueden probar con el siguiente experimento:
Midan la mayor distancia entre una pared y su correlativa paralela dentro de su sala. Podría ser la pared
frontal (la que miran cuando están sentados frente a los monitores) y la pared trasera y llamemos a esa
dimensión:

L (Longitud)

Queda claro que esto va a depender de cada caso en particular.

Dividan 172 entre L, el resultado es la frecuencia de resonancia a la que llamaremos Fr, o sea la formula
completa es:

Fr = 172 / L

Nota: Esa frecuencia es lo que se llama modo axial y en este caso es el modo más bajo correspondiente a la
longitud de tu sala.

Por ejemplo, si la distancia entre paredes frontal y trasera es de 4 metros y 20 centímetros nuestra frecuencia
de resonancia o modo axial más bajo es:

172 / 4.20 mts = 40.95 Hertz, por lo tanto

Fr = 40.95 Hz, que corresponde más o menos la nota Mi más grave de un bajo eléctrico

Con algún programa de edición de audio generen una frecuencia de exactamente del valor Fr que obtuvieron
para su cuarto y accionen play.

Una nota grave empezará a sonar. En su consola bajen o muteen el volumen de uno de los lados, L o R es
igual, lo importante es que la señal sólo salga por una sola bocina. Cierren puertas y ventanas.

Tápense un oído con el dedo y caminen por todo el cuarto. Inmediatamente escucharan los agujeros.
Agáchense al caminar y súbanse a una silla, si buscan con cuidado cerca del centro del cuarto encontrarán que hay un punto donde no se escucha absolutamente nada y otros al fondo del cuarto, cerca de las esquinas donde se oye fuertísimo.

¿Convencidos? Pues bien, si nuestra cabeza estuviera situada en un nodo o “agujero” a la hora de mezclar,
intuitivamente subiremos los graves de la mezcla para compensar, provocando que al sacar la mezcla del
estudio ésta quede demasiado grave.

Por el contrario, si nuestra cabeza estuviera en un antinodo, escucharemos demasiados graves, tenderemos a
bajarlos y la mezcla quedara muy aguda, sin bajos, o con bajos poco definidos.

El mismo fenómeno ocurriría al colocar un micrófono dentro de una sala.

El tema es que no sabemos dónde estamos ubicados. No contamos con ninguna referencia visual. ¿Se
entiende?

No imaginen esta situación solo en una Sala de Control o de Edición o de Mastering, donde generalmente las posiciones (fuentes – receptores) son relativamente fijas. Imagínense esta situación también en recintos donde las fuentes y receptores son varios. Por ejemplo en un Estudio hay múltiples fuentes y micrófonos distribuidos aleatoriamente dentro de la sala. O en una sala de espectáculos donde los oyentes están distribuidos en diferentes sectores del local (¿qué escuchará cada uno?, ¿qué escuchará el sonidista, encargado de realizar la mezcla correspondiente?, ¿qué estará captando un micrófono en una posición determinada?). Bueno, como dijimos anteriormente, todo depende de donde estén ubicados (micrófonos u oyentes) dentro de la sala y de cuál sea la composición modal de la misma en ese punto específico. En sí, es una lotería.

Existe el mito de que las paredes anguladas (para evitar paralelismo) eliminan los modos dentro de una sala.
Esto es absolutamente falso, ya que siempre que tengamos un sonido emitiéndose dentro de un cuarto cerrado, los problemas de fase van a existir. Entonces, la pregunta es: ¿qué hacemos con ellos?

Por suerte en este artículo mostraremos una forma fácil de calcular los modos de una sala con forma
paralelepípeda (paredes paralelas) y lograr que la respuesta modal de la misma sea correcta.

En conclusión: no hay que temerles a las paredes paralelas siempre y cuando respetemos lo enunciado a
continuación:

Debido a que todos estos inconvenientes se deben a la relación entre las tres dimensiones del cuarto, la forma más práctica de disminuir estos problemas es lograr una buena relación entre Largo, Ancho y Altura usando una fórmula que nos permite identificar las frecuencias modales de nuestra sala o, si no, recurriendo a los ya probados Golden Ratios.

Cálculo de modos axiales, tangenciales y oblicuos

La frecuencia de cualquier modo se puede obtener de la siguiente fórmula:

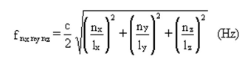
Donde:
nx: 0, 1, 2, 3, … n: [número entero]

ny: 0, 1, 2, 3, … n: [número entero]

nz: 0, 1, 2, 3, … n: [número entero]

Lx: Eje mayor de la sala

Ly: Eje mediano de la sala

Lz: Eje menor de la sala

Las diferentes combinaciones de “nx”, “ny” y “nz” proveen la frecuencia de los modos calculados.

Por ejemplo:

nx=1, ny=0, nz=0 - modo (1,0,0) – modo axial correspondiente a la longitud de la sala.

nx=0, ny=1, nz=0 - modo (0,1,0) – modo axial correspondiente al ancho de la sala.

nx=0, ny=0, nz=1 - modo (0,0,1) – modo axial correspondiente a la altura de la sala, suponiendo que esa sea la dimensión menor.

Existen diferentes combinaciones de enteros que pueden usarse para los cálculos. Los primeros modos son
asociados con valores 1. Los segundos modos son asociados con valores 2. Los terceros modos son asociados con valores 3, y así……

Estos enteros no solo proveen la clave para hallar la frecuencia de un modo, sino que también sirven para
identificarlos como axiales, tangenciales u oblicuos. Como regla general, podemos decir que con dos ceros
(0,3,0) es identificado un modo axial, con un cero (2,0,3) es identificado un modo tangencial y con ningún
cero (1,4,2) es identificado un modo oblicuo.

Para cálculos en metros:

Velocidad del sonido (C)= 344m/s

Lx (eje mayor): [m]

Ly (eje medio): [m]

Lz (eje menor): [m]

Para cálculos en pies:

Velocidad del sonido = 1130ft/s

Lx (eje mayor): [ft]

Ly (eje medio): [ft]

Lz (eje menor): [ft]

Ahora ¡a trabajar! Tomá las medidas de tu cuarto, reemplazá esas dimensiones en la fórmula mencionada y
calcula la respuesta modal de tu sala.

Conclusiones

La respuesta de un local debe ser lo más neutra posible y para esto es necesario que el número de frecuencias características sea elevado y su distribución lo más regular posible.

Por el contrario, cuando hay una concentración de modos en una banda estrecha, se produce coloración del sonido.

Las frecuencias o modos normales de vibración de un recinto, están separados en un espectro más denso, o sea, el campo sonoro es más constante si la longitud, anchura y altura de una sala no son iguales ni múltiplos unos de otros. (Las salas cúbicas son las de peor respuesta modal.)

Optimizar las relaciones de dimensiones dentro del cuarto a fin de mejorar la respuesta modal de la sala va a lograr que sea menos necesario el uso de trampas de baja frecuencia y resonadores, ahorrando espacio y dinero.

Tengan paciencia y hagan el experimento. Aprenderán muchísimo de acústica si logran escuchar los nodos y antinodos de su cuarto. Solo hay que hacer una cuenta de dividir.

Tips: Si tus bocinas son pequeñas o no reproducen muy bien la frecuencia de resonancia calculada, multiplica la frecuencia por 2 y volvé a intentarlo.

Además de experimentar con la fórmula mencionada, también pueden recurrir a muchos de los Golden Ratios publicados en varios artículos o bibliografía donde también pueden escoger entre alguno de ellos y obtener una buena relación dimensional para tu sala.

¡Buena suerte!